Introduction
The PEARL model (Pesticide Emission Assessment at Regional and Local scales) describes the fate of pesticides in the plant-soil system and it is coupled to the hydrological model SWAP (Soil Water Atmosphere Plant). Meteorological data on an hourly or daily basis are needed. Soil water flow is calculated using established methods. Different groundwater regimes, irrigation methods and various drainage pathways to water courses can be simulated by SWAP.
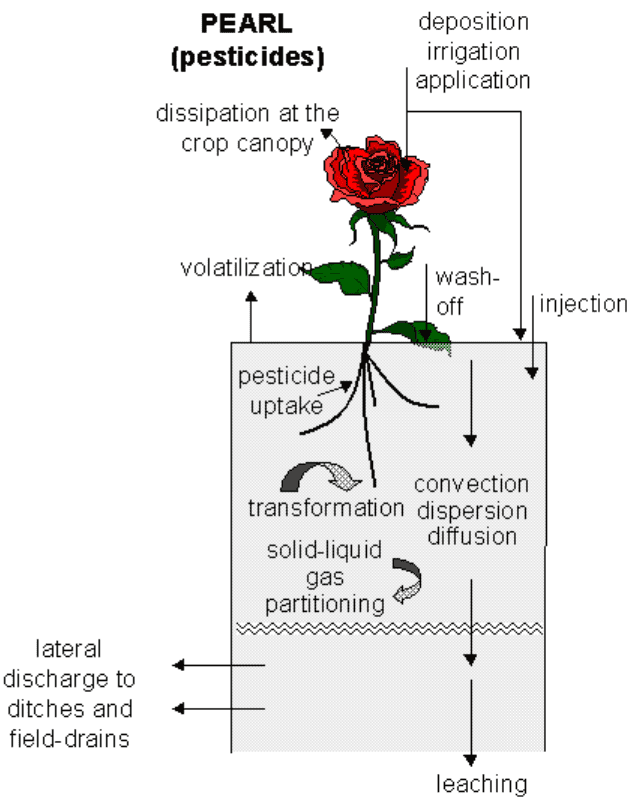
The pesticide can enter the plant-soil system directly by application or indirectly by atmospheric deposition. The fate of the product is described based on concepts for transport processes in the soil system, equilibrium sorption, non-equilibrium sorption, volatilisation, lateral discharge, transformation and preferential flow.
Soil-water interactions
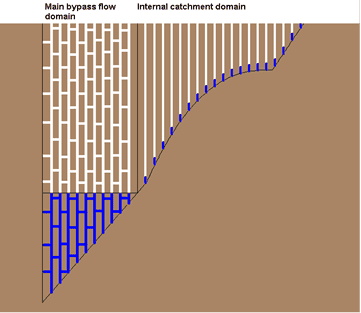
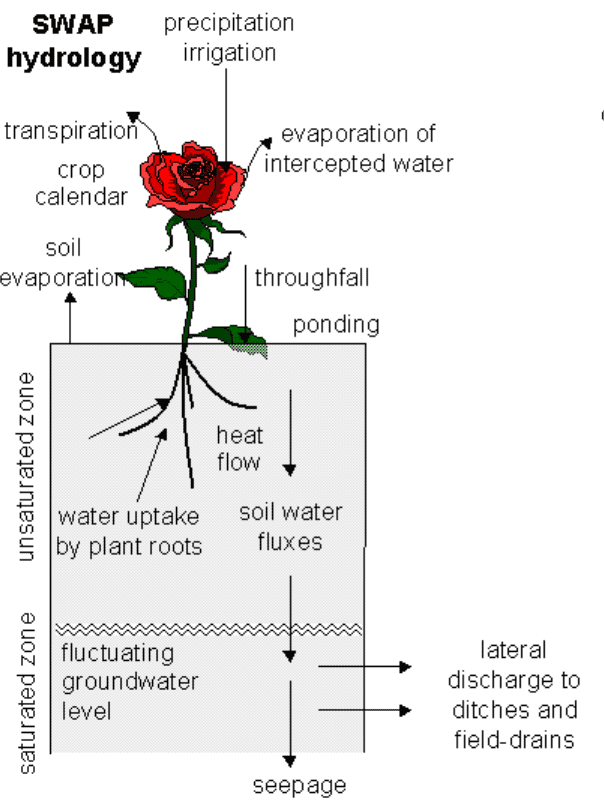
Soil water flow is described with the SWAP model. SWAP (Soil, Water, Atmosphere and Plant) simulates vertical transport of water and heat in unsaturated/saturated soils. The model is designed to simulate flow and transport processes at field scale level, during growing seasons and for long term time series. Water flow in soil is described by Richard’s equation including a range of possible lower boundary conditions (for instance groundwater levels that fluctuate in response to the rainfall input). Soil evaporation and plant transpiration is calculated via multiplying a reference evapotranspiration rate with soil and crop factors. In the context of PEARL, crop growth is usually simulated with a simple growth model that assumes a fixed length of the growing season. In this growth model, both the leaf area index and the rooting depth are a function of the development stage of the crop. However, the generic crop growth module WOFOST is incorporated as well in SWAP and can be used simulate leaf photosynthesis and crop growth. Heat flow in soil is described with Fourier’s law. The thermal properties are a function of porosity and water content and are therefore a function of time and soil depth. The macropore module in SWAP includes infiltration into macropores at the soil surface, rapid transport in macropores to deeper layers, lateral infiltration into and exfiltration out of the soil matrix, water storage in macropores, and rapid drainage to drainage systems. The macropores are divided in a main bypass domain (network of continuous, horizontal interconnected macropores) and an internal catchment domain (discontinuous macropores ending at different depths). The internal catchment domain causes infiltration of macropore water at different, relatively shallow depth. In addition, the macropores are divided in static and dynamic volumes. The dynamic volumes depend on shrinkage characteristics.
Fate and behaviour of substances
PEARL is based on: (i) the convection/dispersion equation including diffusion in the gas phase with a temperature dependent Henry coefficient, (ii) a two-site Freundlich sorption model (one equilibrium site and one kinetic site), (iii) a transformation rate that depends on water content, temperature and depth in soil, (iv) a passive plant uptake rate. The model includes formation and behaviour of transformation products and describes also lateral pesticide discharge to drains. PEARL can simulate preferential flow. Volatilisation from the soil surface is calculated assuming a laminar air layer at the soil surface. PEARL uses an explicit finite difference scheme that excludes numerical dispersion (the dispersion length was set to 5 cm). Below some more detailed information on the different processes simulated by PEARL is given.
Pesticide application and deposition
Pesticides can enter the system by direct application or by atmospheric deposition. The application methods described in PEARL are spraying of pesticide on the soil surface, spraying on the crop canopy, incorporation of pesticide into the topsoil (e.g. by rotor tillage), and injection of pesticide into the topsoil.
Vertical transport of pesticides
Transport of the pesticide in the liquid phase of the soil is described by an equation including convection, dispersion and diffusion. The dispersion coefficient is taken to be proportional to the soil water flux. The diffusion coefficient is a function of the soil water content. The model contains three options to describe the relative diffusion coefficient. Transport in the gas phase is described by Fick’s law. The diffusion coefficient is a function of the volume fraction of the gas phase. The model contains three options to describe the relative diffusion coefficient, including the function of Millington and Quirk (1960).
Lateral discharge of pesticides
The rate of water discharged by the tile-drainage system is calculated by the hydrological submodel. The lateral discharge of pesticides is taken proportional to the water fluxes discharged by the tile-drainage system. PEARL output can be taken as input for the TOXSWA model.
Volatilization of pesticides
In the current model version, different model concepts of volatilisation have been implemented. A simple approach is based on the diffusion of vapour through the soil and a laminar air-boundary layer (cf. Jury et al., 1990). A more advanced concept is based on the concept of a resistance to transport of pesticide from the surface into the atmosphere (Wang et al., 1997; Asman, 1998). As the volatilisation from soil depends on the moisture condition at the soil surface, the effect of increased sorption to the soil particles under dry soil conditions has been implemented into the model.
Partitioning of pesticides
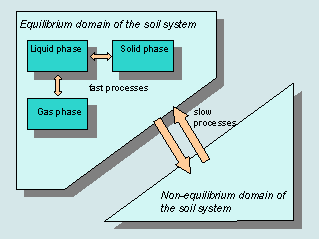
PEARL considers a three phase system. The sorption of pesticide on the solid phase is described with a Freundlich-type equation. In the most common approach, the Freundlich coefficient is calculated on the basis of the coefficient of equilibrium sorption on organic matter, Kom. PEARL contains an option of pH dependent sorption. If this option is used, the dissociation constant, pKa, must be specified. The partitioning of the pesticide between the gas phase and the liquid phase is described by Henry’s law. Pesticide sorption to the non-equilibrium phase is described by a first-order rate equation. This equation requires a desorption rate coefficient.
Non-equilibrium sorption
Simulation of the increase of sorption in time is one of the options in higher tiers of pesticide regulatory leaching assessments in the EU to obtain more realistic leaching estimates. PEARL assumes a Freundlich two-site sorption submodel to describe non-equilibrium sorption. The submodel assumes two types of sorption sites: equilibrium sites and non-equilibrium sites. The sorption isotherms for both sites are described with Freundlich equations. The content sorbed at the equilibrium site is assumed to be continuously at equilibrium and the content sorbed at the non-equilibrium site is described with a pseudo first-order sorption rate equation.
The model requires accurate estimates of non-equilibrium sorption parameters. Estimates of these parameters can be obtained with inverse modelling techniques and using long-term sorption experiments. For this purpose the PEARLNEQ software is developed. PEARLNEQ contains the same two-site model as implemented in the PEARL model.
Pesticide transformation
Transformation of pesticides may lead to reaction products (daughters) that may show a certain degree of persistence and mobility in soils. For this reason, the formation and behaviour of the most important daughters is included in PEARL. Transformation of the individual compounds is described with first-order kinetics. The rate of pesticide transformation in soil depends on temperature, soil moisture content and depth in soil. A compound residing in the non-equilibrium domain is not subject to transformation, which implies that the half-life of transformation refers to the equilibrium domain only. An important consequence is that the transformation half-life, which usually refers to the total mass content, should be obtained in a special procedure.
Preferential pesticide transport
The transport of PPPs in macroporous soils is described for the soil matrix and two preferential flow domains, i.e. a bypass domain and an internal catchment domain (Kroes et al. 2008). Macropores can be either permanent or temporary (due to shrinking of soils).
In SWAP, macropore geometry is described on the basis of three properties, i.e. continuity, persistency and macropore shape. The main bypass flow domain is a network of continuous, horizontally interconnected macropores. These macropores penetrate deep into the soil profile and are assumed to be horizontally interconnected. In the main bypass domain, water is transported fast and deep into the soil profile, bypassing the soil matrix. This may lead to rapid drainage towards drainpipes and short-circuiting between the soil surface and the groundwater. The internal catchment domain consists of discontinuous, non-interconnected macropores ending at different depths in the profile. In this domain, water is captured at the bottom of individual macropores, resulting in forced infiltration of macropore water into the soil matrix.